- Outeur Stanley Ellington ellington@answers-business.com.
- Public 2023-12-16 00:12.
- Laas verander 2025-01-22 15:51.
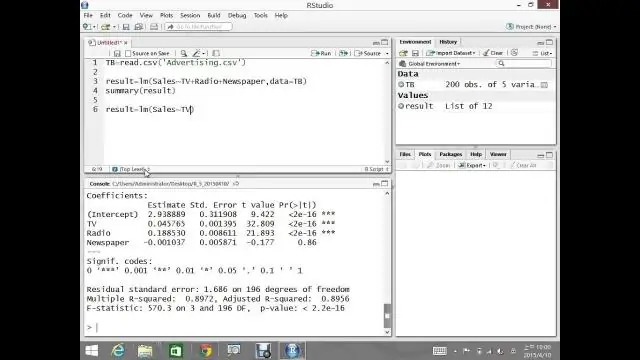
Veelvuldige lineêre regressie is 'n uitbreiding van eenvoudig Lineêre regressie gebruik om 'n uitkomsveranderlike (y) te voorspel op grond van veelvoudig duidelike voorspellerveranderlikes (x). Hulle meet die verband tussen die voorspellerveranderlike en die uitkoms.
Dan, wat beteken die veelvoud R in 'n regressie?
Veelvuldige R . Hierdie is die korrelasiekoëffisiënt. Dit vertel jou hoe sterk die lineêre verhouding is is . Byvoorbeeld, 'n waarde van 1 beteken 'n perfekte positiewe verhouding en 'n waarde van nul beteken glad geen verhouding nie. Dit is die vierkantswortel van r vierkantig (sien #2).
Weet ook, wat beteken 'n R-kwadraatwaarde? R - vierkantig is 'n statistiese maatstaf van hoe naby die data aan die aangepaste regressielyn is. Dit staan ook bekend as die koëffisiënt van bepaling, of die koëffisiënt van meervoudige bepaling vir meervoudige regressie. 100% dui aan dat die model al die veranderlikheid van die responsdata rondom sy verduidelik beteken.
Net so, wat is lineêre regressie in R?
Lineêre regressie word gebruik om die waarde van 'n kontinue veranderlike Y te voorspel gebaseer op een of meer insetvoorspellerveranderlikes X. Die doel is om 'n wiskundige formule tussen die die responsveranderlike (Y) en die voorspellerveranderlikes (Xs) daar te stel. Jy kan hierdie formule gebruik om Y te voorspel, wanneer slegs X-waardes bekend is.
Wat is die verskil tussen R en R 2 in statistiek?
R ^ 2 = ( r )^ 2 d.w.s. (korrelasie)^ 2 . R vierkant is letterlik die vierkantig van korrelasie tussen x en y. Die korrelasie r vertel die sterkte van lineêre assosiasie tussen x en y aan die ander kant R vierkant wanneer dit in regressiemodelkonteks gebruik word, vertel dit van die hoeveelheid veranderlikheid in y wat deur die model verduidelik word.
Aanbeveel:
Wat is lineêre regressie Python?
Lineêre regressie (Python -implementering) Lineêre regressie is 'n statistiese benadering vir die modellering van 'n verband tussen 'n afhanklike veranderlike met 'n gegewe stel onafhanklike veranderlikes. Let wel: In hierdie artikel verwys ons afhanklike veranderlikes as reaksie en onafhanklike veranderlikes as kenmerke vir eenvoud
Wat is die vergelyking vir meervoudige regressie?

Meervoudige regressie. Meervoudige regressie verduidelik oor die algemeen die verband tussen veelvuldige onafhanklike of voorspellerveranderlikes en een afhanklike of kriteriumveranderlike. Die meervoudige regressievergelyking wat hierbo verduidelik word, neem die volgende vorm aan: y = b1x1 + b2x2 + … + bnxn + c
Wat is die lineêre regressie van die data?
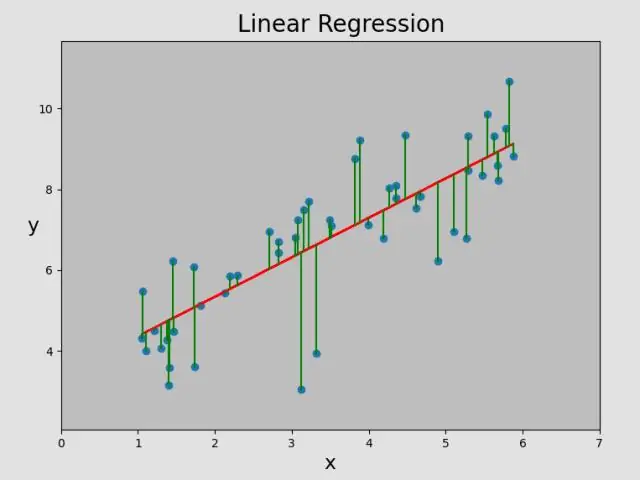
Lineêre regressie poog om die verwantskap tussen twee veranderlikes te modelleer deur 'n lineêre vergelyking by waargenome data te pas. 'n Lineêre regressielyn het 'n vergelyking van die vorm Y = a + bX, waar X die verklarende veranderlike is en Y die afhanklike veranderlike is
Wat sê meervoudige regressie vir jou?

Meervoudige regressie is 'n uitbreiding van eenvoudige lineêre regressie. Dit word gebruik wanneer ons die waarde van 'n veranderlike wil voorspel op grond van die waarde van twee of meer ander veranderlikes. Die veranderlike wat ons wil voorspel word die afhanklike veranderlike genoem (of soms die uitkoms-, teiken- of kriteriumveranderlike)
Hoe doen jy meervoudige lineêre regressie?

Om 'n verband te verstaan waarin meer as twee veranderlikes teenwoordig is, word 'n meervoudige lineêre regressie gebruik. Voorbeeld Gebruik veelvuldige lineêre regressie yi = afhanklike veranderlike: prys van XOM. xi1 = rentekoerse. xi2 = olieprys. xi3 = waarde van S&P 500-indeks. xi4= prys van olie-termynkontrakte. B0 = y-afsnit op tyd nul
